机器学习中很多时候都是在求解无约束条件的最优化问题,比如:感知机、逻辑斯谛回归、条件随机场的求解。在求解无约束最优化问题最常用的两类方法是 梯度下降法 和 牛顿法,可参考《统计学习方法》的附录A 和 附录B。 这篇笔记记录下自己对两类方法的理解。
梯度下降法
在机器学习任务中,要求目标函数 $f(x)$ 的使其最小的 $x$ 的值。梯度下降是一种迭代算法,常用来求解这类问题。基本步骤为:选取初值;梯度方向不断迭代;更新 $x$ 的值找到最逼近的解。
选取
$x^{k}$,计算$f(x^{k})$,$k$初始值为0;将
$f(x^{k+1})$在$x^{k}$处一阶泰勒展开得:$f(x^{k+1}) = f(x^{k} + \Delta t) \approx f(x^{k}) + f'(x^{k}) \Delta t$,按梯度方向不断迭代逼近可取$\Delta t = - \lambda \cdot f'(x^k)$,其中$\lambda$为步长;重复以上两步,直到迭代找出相应的
$x^{k+1}$为止,即$||f(x^{(k+1)} - f(x^k) || < \epsilon$,停止迭代,令$x=x^{k+1}$;
个人理解:$\Delta t = - \lambda \cdot f'(x^k)$ 这里的 $\lambda$ 为步长,可由一维搜索确定(比如GBDT);也可直接赋一个小的数即可(比如神经网络模型)。
牛顿法
牛顿法是二阶泰勒展开,而梯度下降法是一阶泰勒展开。其基本步骤如下:
选取
$x^k$,计算$f(x^k)$,$k$初始值为0;将
$f(x^{k+1})$在$x^k$处二阶泰勒展开得:$f(x^{k+1}) = f(x^k + \Delta t) \approx f(x^k) + f'(x^k) \cdot \Delta t + \frac{1}{2} \cdot f''(x^k) \cdot (\Delta t)^2$,通常将一阶导和二阶导分别记为$g$和$h$:$f(x^{k+1}) \approx f(x^k) + g \cdot \Delta t + \frac{1}{2} \cdot h \cdot (\Delta t)^2$,因为要使$f(x^{k+1})$取得极小值,则令$\frac{ \partial ( g \Delta t + \frac{1}{2} h \Delta t^2 ) } {\Delta t} = 0$,得到$\Delta t = - \frac{g}{h}$,则$x^{k+1} = x^{k} - \frac{g}{h}$,按二阶梯度方向不断迭代逼近;重复以上两步,直到迭代找出相应的
$x^{k+1}$为止;
注:当参数 $x^k$ 推广到向量形式,迭代公式 $x^{k+1} = x^k - H^{-1} \cdot g$ ,这里 $H$ 是海赛矩阵。
个人理解:这里统计学习方法里没有引入 $\lambda$ 步长,这里是可以加上 $\lambda$ 步长,在很多机器学习框架里已经加入了步长(比如XGBoost中的eta参数);
区别
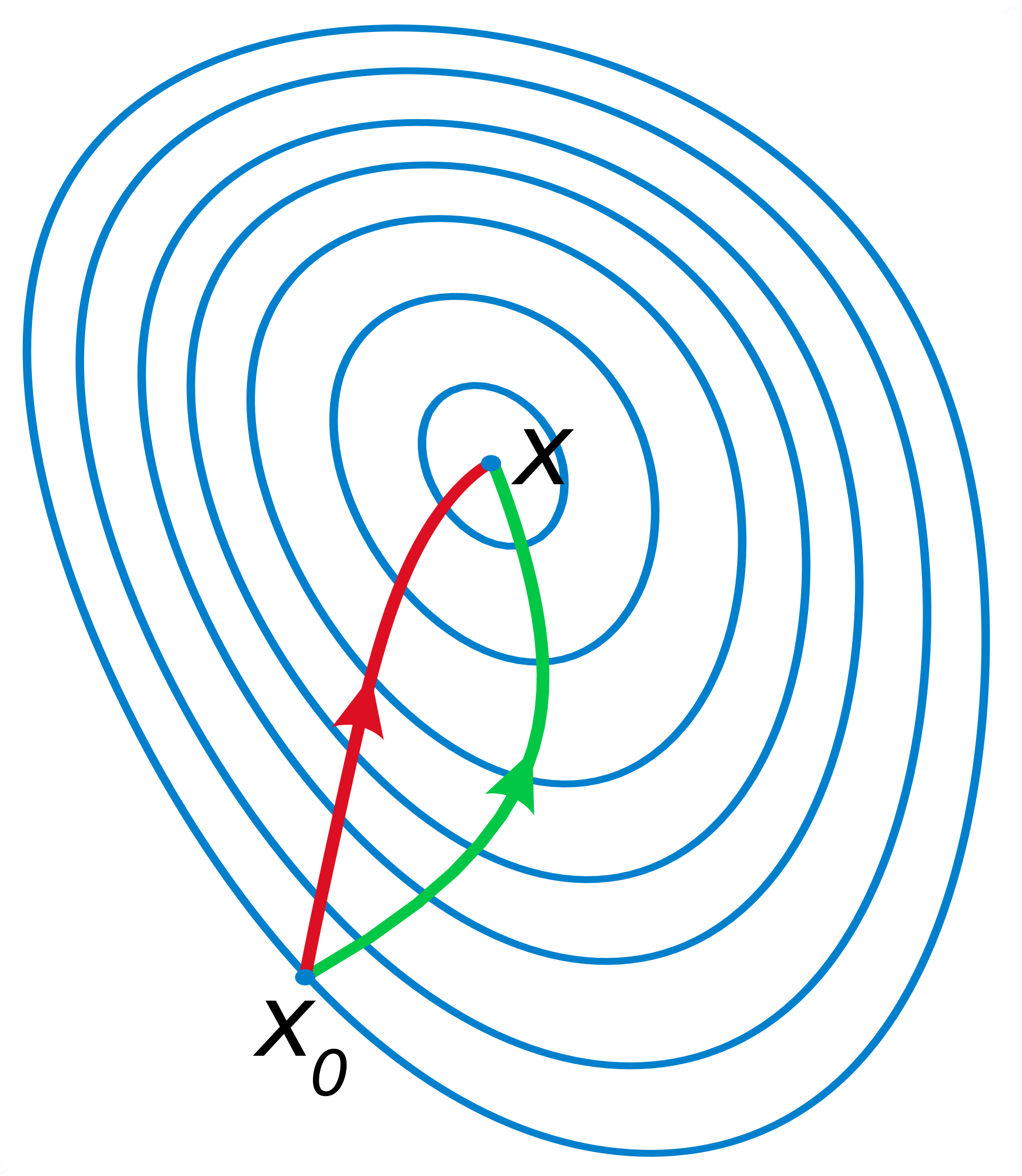
梯度下降是一阶收敛,牛顿法是二阶收敛,牛顿法相比梯度下降收敛更快。
如果更通俗点,比如你想找一条最短路径到一个盆地的最底部,梯度下降每次从你当前所处位置选一个坡度最大的方向走一步;而牛顿法在选择方向时,不仅会考虑坡度是否大,还会考虑当你走了一步后,坡度是否会变得更大。所以说牛顿法比梯度下降法看得更远一点,能更快地到达盆地的最底部。
从几何上说,牛顿法是用二次曲面去拟合你当前所处位置的局部曲面,而梯度下降是用一个平面去拟合当前的局部曲面,通常情况下,二次曲面的拟合会比局部曲面更好,所以牛顿法选择下降路径会更符合最优的路径。
参考文献
《统计学习方法》附录A 与 附录B