最近在复习机器学习的基础,学习下《统计学习方法》感知机这章,主要针对书上难以理解的部分做一些学习笔记,方便自己后期复习。
感知机是 二分类 的线性分类模型,输入为实例的特征向量,输出为实例的类别(取+1和-1)。感知机对应于输入空间中将实例划分为二类的分离超平面。感知机旨在求出该超平面,为求得超平面引入了基于误分类的损失函数,利用梯度下降法对损失函数进行最优化。
感知机1957年被提出,它是 神经网络模型 与 支持向量机(SVM) 的基础。
感知机模型定义
对于 $x \in R^n$ ,输出 $\{+1, -1\}$ ,表达形式为: $f(x) = sign(w \cdot x + b)$ ,即该式称为感知机。
其中,$sign(x) = \left\{\begin{matrix}
+1, & x \geqslant 0 & \\
-1, & x < 0 &
\end{matrix}\right.$
$sign$ 通常称之为激活函数,激活函数同时也是构成神经网络模型的基本单元,不过在神经网络模型中通常用 $sigmoid$ 函数。
几何含义即对应书上的超平面,如下图。
其实我们就是在学习参数 $w$ 和 $b$ ,确定了 $w$ 和 $b$ ,图上的直线(高维高间下为超平面)也就确定了,那么以后来一个数据点,就可以用训练好的模型进行预测,如果大于等于0就分到 +1,小于0就分到 -1。
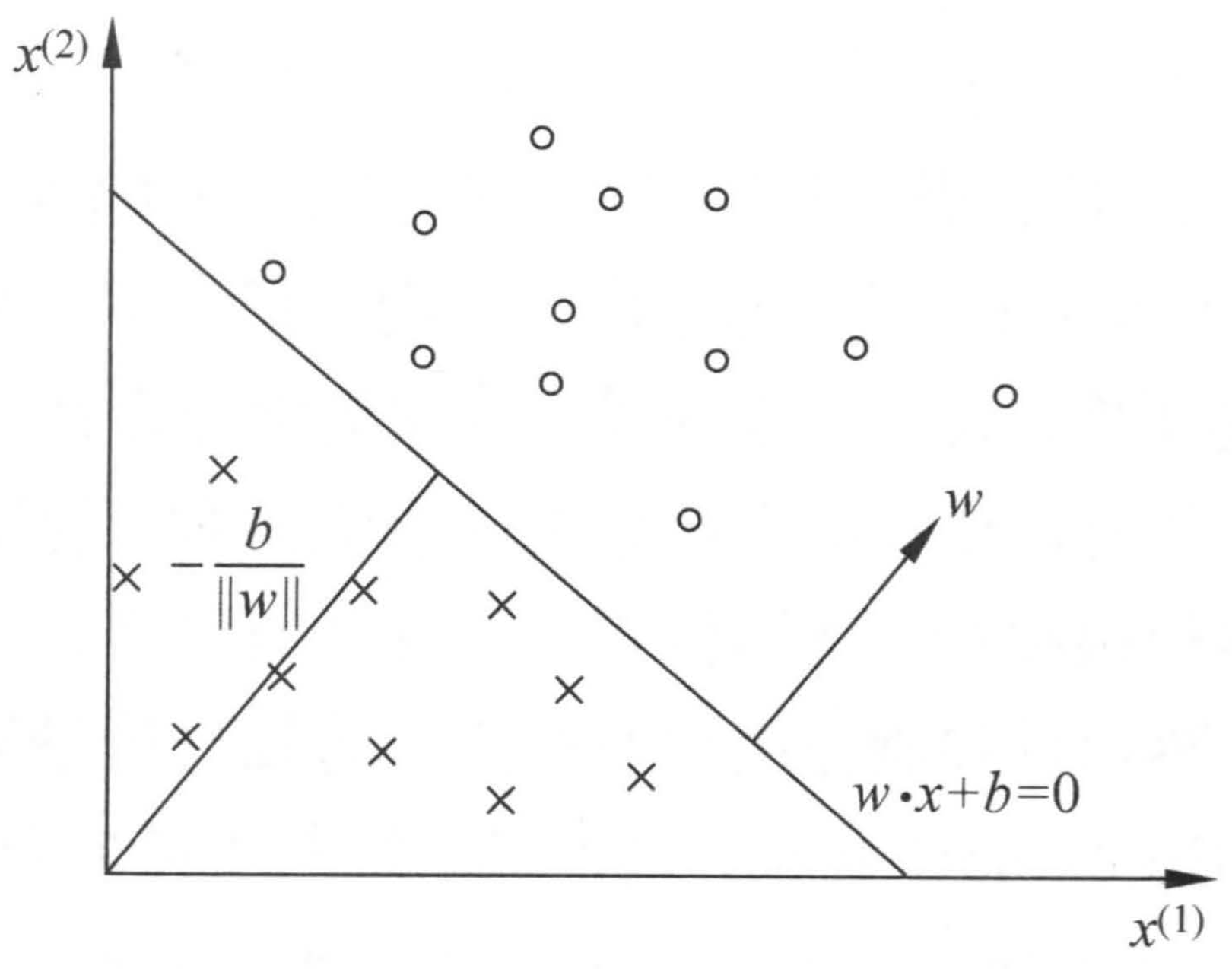
这里有个小知识点(大概是高中的几何数据)证明下,证明如下。
证明: $\overrightarrow{w}$ 是直线 $\overrightarrow{w} \cdot \overrightarrow{x} + b = 0$(高维空间下为超平面)的法向量。
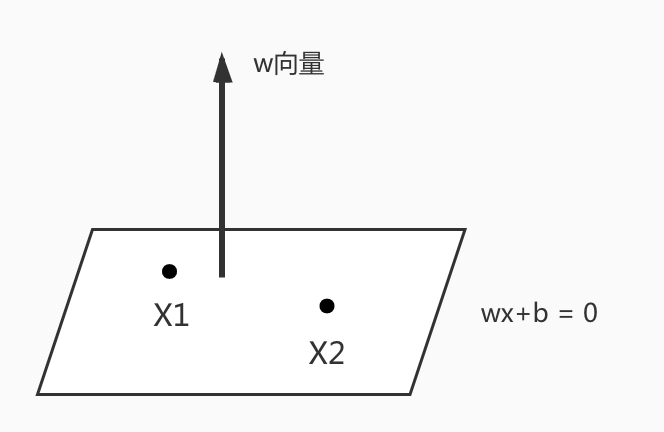
任找平面 $\overrightarrow{w} \cdot \overrightarrow{x} + b = 0$ 上两点 $x_1, x_2$ ,如上图。
则 $\left\{\begin{matrix}
\overrightarrow{w} \cdot \overrightarrow{x_1} + b =0 & 式1 & \\
\overrightarrow{w} \cdot \overrightarrow{x_2} + b =0 & 式2 &
\end{matrix}\right.$
式1 减 式2 得: $\overrightarrow{w} \cdot (\overrightarrow{x_1} - \overrightarrow{x_2}) = 0$ ,即 $\overrightarrow{w} \cdot \overrightarrow{x_2 x_1} = 0$ ,
则 $\overrightarrow{w}$ 与 $\overrightarrow{x_2 x_1}$ 垂直,平面内其它向量也是如此。
即证 $\overrightarrow{w}$ 是直线 $\overrightarrow{w} \cdot \overrightarrow{x} + b = 0$ (高维空间下为超平面)的法向量
$\overrightarrow{w}$ 为平面 $\overrightarrow{w} \cdot \overrightarrow{x} + b = 0$ 的法向量,可以通过举一些例子也可以方便理解此结论。
超平面距原点的距离为 $\frac{b}{||w||}$ ,这个结论也可以通过例子来理解。
感知机学习策略
上面我们已经知道感知机模型了,我们也知道他的任务是解决二分类问题,也知道了超平面的形式,那么下面关键是如何学习出超平面的参数 $w$ 和 $b$ ,这就需要用到我们的学习策略。
我们知道机器学习模型,需要首先找到损失函数,然后转化为最优化问题,用梯度下降等方法进行更新,最终学习到我们模型的参数 $w$ 和 $b$ 。那么,我们开始找感知机的损失函数。
我们很自然地会想到用误分类点的数目来作为损失函数,是的误分类点个数越来越少,感知机本来也是做这种事的,只需要全部分对就好。但这样的损失函数并不是 $w$ 和 $b$ 连续可导(无法用函数形式来表达出误分类的人数),无法进行优化。
于是转为另一种选择,误分类点到超平面的总距离(直观来看,总距离越小越好),则距离公式为 $\frac{1}{||w||} |w \cdot x_0 + b|$ ,
考虑到类别,因为是二分类问题,所以可以进一步化简得:$- \frac{1}{||w||} y_i (w \cdot x_0 + b)$
那么所有误分类点的集合为 $M$ ,则总距离为 $- \frac{1}{||w||} \underset{x_i \in M}{\sum} y_i (w \cdot x_i + b)$
因为 $\frac{1}{||w||}$ 是常数,可以不考虑,所以最终得到损失函数为:$L(w,b) = - \underset{x_i \in M}{\sum} y_i (w \cdot x_i + b)$
感知机学习问题转化为求解损失函数的最优化问题,最优化的方法就是套路的方法,即 随机梯度下降法 。
总结
感知机的模型是 $f(x) = sign(w*x + b)$ ,它的任务是解决二分类问题,要得到感知机模型我们就需要学习参数 $w$ 和 $b$ 。则需要一个学习策略,不断的迭代更新 $w$ 和 $b$ ,所以我们就需要一个损失函数,最终选择误分类点到超平面的距离来表示来得到最终的损失函数。
参考文献
浅析感知机-模型与学习策略 ,知乎
《统计学习方法》,李航