工作已经2年多了,目前面试基本上都是找一些技术栈和业务都是适配自己基因的,很多时候面试都会面一些项目经验,具体项目是怎么做的。然后会出一道题试下基本的代码素养,大概也差不多15~30分钟可以写完,否则自我介绍+项目经验+代码在1个多小时内根本答不完。
下面整理一些简单的代码题,方便自己以后找工作热身做题用。
题1
求最大子数组求和。输入一个整型数组,数组里有正数也有负数。数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值,要求时间复杂度为O(n)。
输入: nums = [-2,1,-3,4,-1,2,1,-5,4];输出: 6。解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
def max_seq(nums):
p_first = 0
p_next = p_first
p_max = p_first
sum_current = 0
sum_max = sum_current
for e in nums:
if p_next < p_first:
p_next = p_first
if sum_current + e <= 0:
p_first = p_next + 1
sum_current = 0
else:
sum_current = sum_current + e
p_next = p_next + 1
if sum_current > sum_max:
sum_max = sum_current
p_max = p_next
return (sum_max, p_first, p_max)
if __name__ == '__main__':
nums = [-2, 1, -3, 4, -1, 2, 1, -5, 4]
sum_max, p_first, p_next = max_seq(nums)
print(sum_max, p_first, p_next, nums[p_first:p_next], sep='\t')
题2
给定字符串和常数k,每2k个字符前k个翻转,后k个不动;
例:inputStr = “abcdefg”。 当k=2时,outputStr=“bacdfeg”,当k=8时,outputStr=“gfedcba”
考常python基础语法,代码如下:
#!/usr/bin/python3
# coding:utf-8
def convert(inputStr, k):
"""
convert string.
"""
outputStr = ""
n = len(inputStr)
i = 0
while i * k < n:
if i % 2 == 0:
outputStr += inputStr[ i*k : (i+1)*k ][::-1]
else:
outputStr += inputStr[ i*k : (i+1)*k ]
i += 1
return outputStr
if __name__ == '__main__':
inputStr = "abcdefg"
# 当 k = 2 时
print(convert(inputStr, 2))
# 当 k = 8 时
print(convert(inputStr, 8))
题3
输入矩阵 m*n,矩阵中每个位置含 一个整数,从左上到右个,每个节点只能向右或者向下。求从左上角至右下角和最小的路径值。
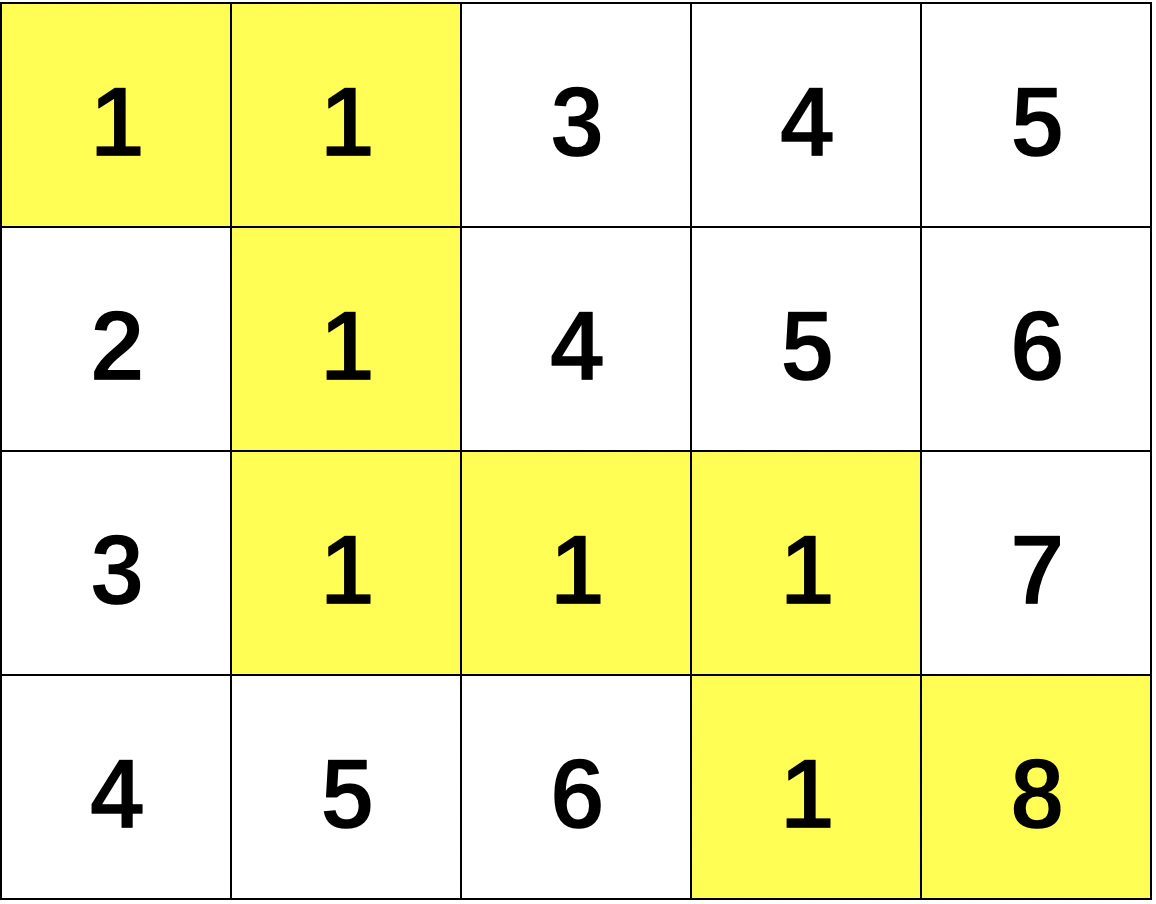
该题题目很好理解,但涉及到的知识点却不少,长时间不刷题,裸写一下子很难想到,主要还是 动态规划 的思想。
面试时,我一开始就想到用DFS搜索的方式来遍历路径了,但题目不需要求路径,况且这样来做会有大量的重复计算;在面试时也想过重复计算状态的保存;但整个思路还是自底向上搜索的方式,陷入了DFS的陷阱中了。
该题最好的思路应该是自顶向下来考虑问题,考虑最后一个状态取决于 左侧 和 上方 两个状态的最小值,即 最优解 = 当前位置 + min(左侧位置,上方位置) ,依次求解,直到左上角;思想类似于 Fibonacci 问题 和 多段图向前实现(github) 。
这里我采用自顶向下的实现,即 (多段图向前推理 或 Fibonacci自顶向下思想),自顶向下经典的实现方式是递归,该题用递归也很好实现,递归会涉及到两个点:1.递归的层次;2.递归的出口 ,这也是递归的难点。
基于上述的思考,整理代码如下:
#!/usr/bin/python3
# coding:utf-8
def dp(m, n, matrix):
"""
DP algorithm.
"""
# 递归的出口
if (m == 0) and (n == 0):
return matrix[m][n]
else:
if (m > 0) and (n > 0):
return matrix[m][n] + min( dp(m-1, n, matrix), dp(m, n-1, matrix) )
elif (m > 0) and (n == 0):
return matrix[m][n] + dp(m-1, n, matrix)
elif (m == 0) and (n > 0):
return matrix[m][n] + dp(m, n-1, matrix)
if __name__ == '__main__':
matrix = [ [1, 1, 3, 4, 5],
[2, 1, 4, 5, 6],
[3, 1, 1, 1, 7],
[4, 5, 6, 1, 8] ]
m = len(matrix) # 行数
n = len(matrix[0]) # 列数
min_path_value = dp(m-1, n-1, matrix)
print(min_path_value)
题4
棋盘大小 n*n,每行、每列、对角线只能放一枚棋子,求所有摆放的情况。
经典的八皇后问题,是算法中 回溯法 的典型例题。采用DFS搜索的方式遍历所有解的可能,在遍历过程中,如果出现了不符合的要求可能,进行限界截断(即place函数),不让其继续搜索。对应的DFS搜索树如右图,搜索顺序为 1->2->3->4->5->6->7->8->9。
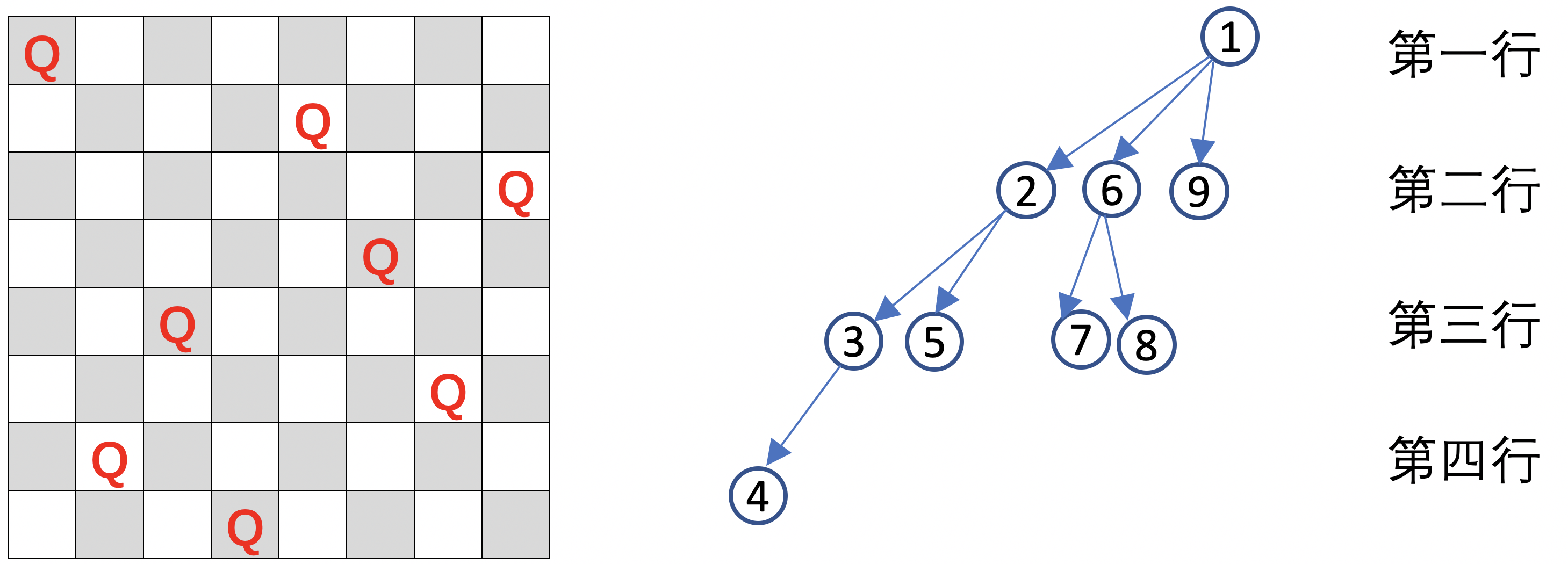
#!/usr/bin/python3
# coding:utf-8
# 回溯法-八皇后问题所有可能
def place(row, column):
"""
如果一个皇后能放在第row行和column[row]列,则返回true;否则返回false。
前row行已放置皇后
"""
i = 0
while i < row:
# 不允许同一列;不允许对角线
if column[i] == column[row] or abs(column[i]-column[row]) == abs(i-row):
return False
i += 1
return True
def n_queen(row, column, n):
"""
n皇后所有解
"""
# 初始化放置第一列
column[row] = 0
while column[row] < n:
if place(row, column):
# 最后一行放置成功
if row == n - 1:
print( column )
else:
# 下一行
n_queen( row + 1, column, n )
# 下一列
column[row] = column[row] + 1
if __name__ == '__main__':
# 棋盘的大小
n = 8
# 棋盘上的行
row = 0
# 初始化,第 row 行,第 column[row] 列放置皇后
column = [0] * n
n_queen(row, column, n)