最近在疏理《统计学习方法》中的知识点,方便自己后续复习。这里记录下第3章K近邻算法的基本思想。
K近邻(KNN)是一种基本分类与回归方法。给定目标样本通过K个邻居来决定目标样本的标签。K近邻法有三个基本要素:K值的选择、距离度量和分类回归决策规则。KNN并不需要训练,但需要遍历整个训练集,所以预测比较慢,书中提到用KD树进行优化,来提高K近邻搜索的效率。
K近邻基本要素
距离度量
KNN一般采用欧式距离,但更一般的是 $L_p$ 距离, $L_p$ 距离在机器学习中经常会看到。
设特征空间 $\chi$ 是 $n$ 维实数向量空间 $R^n$ , $x_i, x_j \in \chi$ , $x_i = (x_i^1, x_i^2, ..., x_i^n)^T$ , $x_j = (x_j^1, x_j^2, ..., x_j^n)^T$ , $x_i, x_j$ 的 $L_p$ 距离定义为
$L_p(x_i, x_j) = (\sum_{l=1}^n |x_i^l - x_j^l|^p) ^{\frac{1}{p}}$ ,其中 $p \geqslant 1$
当 $p = 1$ 时,称为曼哈顿距离,即 $L_1(x_i, x_j) = \sum_{l=1}^n |x_i^l - x_j^l|$ ;
当 $p = 2$ 时,称为欧式距离,即 $L_2(x_i, x_j) = (\sum_{l=1}^n |x_i^l - x_j^l|^2) ^{\frac{1}{2}}$ ,写成我们最熟悉的形式 $\sqrt{(\Delta x_1)^2 + (\Delta x_2)^2 + ... + (\Delta x_n)^2}$ ;
当 $p = \infty$ ,它是各个坐标距离的最大值,即 $L_\infty(x_i, x_j) = \underset{l}{max} \ |x_i^l - x_j^l|$ 。
下图给出二维空间中 $p$ 取不同值时,与原点的 $L_p$ 距离为1( $L_p = 1$ )的点的图形。
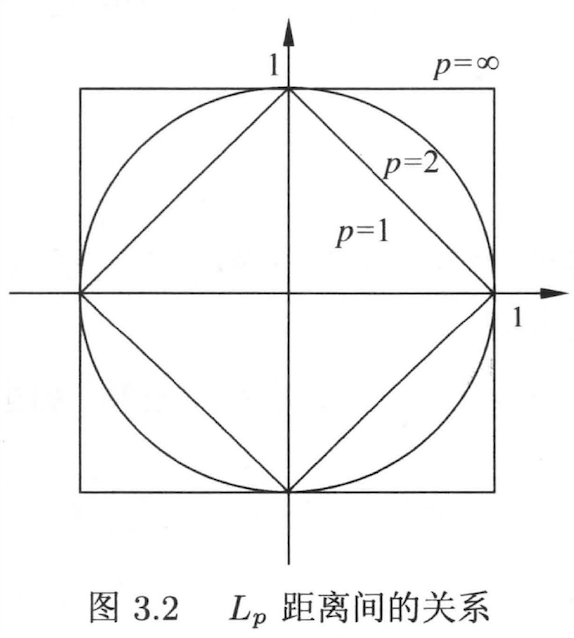
由上图,我们可以从直观看出 $L_p$ 当 $p$ 取不同值时的一些性质,当 $p=2$ 时即欧式距离(也称L2范式),相比平滑很多,而且可导。正因为它的平滑性和可导性,在机器习学中大量使用 L2 范式:作为损失函数(又名最小二乘法误差,即least squares error, LSE)、作为正则项(即 $\lambda \sum_{i=1}^k (w_i)^2$ )。
K值选择和决策
K值选择会对KNN的结果产生很大影响。K既不能太小也不能太大。如果选择较小的 $K$ 值,极端取 $K=1$ 就意味着模型变得复杂,容易发生过拟合;如果选择较大的 $K$ 值,极端取 $K = N$ ( $N$ 即为样本的数量),那么模型过于简单(容易欠拟合)。书上用了近似误差(关注的是训练集)和估计误差(关注的是测试集即泛化性)来描述的,知乎上有关于近似误差和估计误差的详细解释(链接)。
在实际应用中, $K$ 值先取一个较小的数值,再逐渐增大。可采用交叉验证来选取最优的 $K$ 值。
KNN在分类问题中往往是多数表决,即由输入实例的K个邻近的训练实例中的多数类决定最终结果;
KNN在回归问题中是取平均,即对样本的K个邻近标签值取平均,作为预测结果。
KD树
K近邻算法如果用线性扫描,则时间复杂度为 O(N),当训练集很大时,计算非常耗时;所以为了提高K近邻搜索效率,使用特殊的存储结构(即KD树),以减少扫描的次数,时间复杂度为 O(logN);可以理解为用空间换时间,空间体现在存储结构的构建,这种“空间换时间”的思想在机算机科学里屡见不鲜。
KD树需要 先构造,再搜索,注意这里的 “KD树的K” 和 “K近邻的K” 含义不同,这里的K是指数据的维度。
KD树构造
输入:样本集 $X = \{x_1, x_2, x_3, ..., x_n\}$ ,其中 $x_i = \{x_i^1, x_i^2, ..., x_i^m\}$ , $m$ 是指特征维度(和KD树中的K是相同的含义),为了和K近邻的K区分开,这里用m代替。
构造根结点,即首次 $m=1$ ,根据第一维特征的大小将所有样本排序,以中位数为中心将样本分为两类,分别作为根节点的左右子树;
对于左右子树,分别选取 $m=\{2,3,...,m\}$ 维特征按照中位数进行子树的划分;若叶子结点有多个样本,重复选取 $m=\{1,2,...,m\}$ 再切分样本空间,直至每个叶子结点仅有一个样本为止。
注:假设深度为 $j$ ,则结点选择维度为 $l=(j\%m + 1)$ 的中位数进行切分,取模是个循环重复的过程,直至每个叶子仅有一个样本。
KD树搜索
从根结点 自顶向下 基于树的二分查找找到到叶子结点;从找到的叶子结点 自底向上 找出K个最相邻的样本,自底向上查找的过程可参考下《统计学习方法》书上的例子(直接看算法描述有点晦涩难懂)。
整个时间复杂度是 $2 \times O(logN)$ (自顶向下 和 自底向上 均为 O(logN)),最以最终时间复杂度为 O(logN)。
总结
这里总结了下KNN算法,它的三个基本要素(即距离度量、K值选择和决策),以及KNN的一个经典实现(KD树)。后续学习下KNN的的另一个实现(Ball树),它和KD树的问题出发点相似,都是用空间换时间来解决时间复杂度问题。
KNN的理论比较通俗易懂,后续有空可以尝试些代码的实践,KNN的包在sklearn里有集成( 链接 )。
参考文献
- l1正则与l2正则的特点是什么,各有什么优势? ,知乎
- 《统计学习方法》第3章-K近邻法,李航
- 统计学习方法-K近邻算法 ,CSDN